by David Appell , Phys.org

A team of scientists have invented a new technique to determine the dynamics of microscopic interacting particles by using image recognition to count the number of particles in an imaginary box. By changing the size of the observation box, such counting enables the study of the dynamics of the collective system, even for a dense group of particles suspended in a fluid.
Their work has been published in Physical Review X.
For over a century, scientists of all kinds have sought to exploit counts of particles, such as molecules undergoing Browning motion in a liquid, something scientists in many disciplines would like to know, from biology studying cells to chemists studying molecules to physics.
A useful way to characterize this motion is via the “diffusion constant,” which describes how fast the average particle in the fluid moves. This number can be calculated by following an individual particle as it randomly walks through the fluid. The diffusion constant is then half the proportionality constant between the average displacement and time.
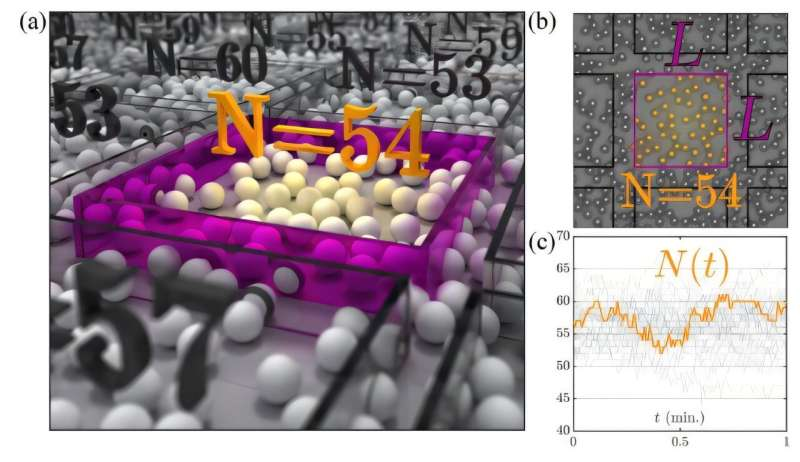
To address this limitation, Sophia Marbach of Sorbonne Université in Paris and her colleagues invented a technique they call the “countoscope.” It uses image recognition software to count the number of particles in an imaginary box in the sample, which can be in the thousands.
The system of particles could be a colloid—particles suspended in a liquid—or cellular organisms, or even artificial. The number of particles in these boxes—finite observation volumes—can change as particles move into or out of the field of view, much like they do in a microscope. The user can select the size of the countoscope box desired in order to study the particles’ dynamics at larger or smaller scales.
But following particle paths and displacements can be difficult, if not impossible, if there are a large number of particles and/or they are indistinguishable.
To address this, the group developed an equation that instead used fluctuating particle counts in the boxes, which can also be used to calculate the diffusion constant and to infer the dynamic properties of the interacting particle suspensions. That constant can then be deduced simply by counting and calculating.
The group tested their technique on a two-dimensional layer of 2.8-micron diameter plastic spheres in a cell filled with water. Using this artificial colloidal system, they choose square boxes with sides from 4- to 32-microns long. The boxes were imaged by a custom-built inverted microscope. Their software then counted, box by box, the number of particles in each box.
With this data they could calculate the mean change in particle number relative to the first box, which they found increased as the square root of time. By this methodology, their value for the diffusion constant matched that obtained from more traditional methods that reconstruct particle trajectories.
When they increased the number of particles in their simulated colloid, particles diffused away from their starting points, as was expected. Their method still worked, but they began to see the formation of temporary bunches of particles, about 10 or so, in their prototype setup. This was something not seen in traditional studies, simply because tracking only a single particle at a time cannot reveal bunches.
While the particles did not interact in their prototype colloid, real world experiments usually cannot be approximated as a noninteracting system. Unlike less dense systems (specified by the “packing fraction” of the spheres), the team found that significant deviations from their mathematical expressions took place at high packing fractions.
This was due to interactions between particles, and they were able to modify their analysis when both hydrodynamic and/or steric factors complicated the system. (Hydrodynamic effects are those induced by the particles’ movement through the fluid, and steric effects arise from the spatial arrangement of the particles.)
In fact, a new length scale appeared in their analysis, characterizing a transition between hyperuniform-like particle behavior and collective states.
The groups believe their methodology can be extended. “We trust our analytical approach can be extended to 3D [three-dimensions], to solids or crystals,” they wrote in their paper.
“We definitely have received interest in use by other scientists,” said Marbach. “It’s such an easy thing to do actually that some colleagues just tried it on their own data and could see similar or different things depending on the system they were investigating.”
She continued, “Many scientists would like to use the framework to investigate very diverse systems beyond colloids: microalgae, bacteria, active colloids, colloidal glasses, molecules, etc.,” she said.
She said there are many directions for future research—to improve the countoscope technique, expand it and generalize it to “include the possibility of probing different dynamical features beyond diffusion. For instance, in microalgae/bacteria/active colloids, we need to know how to resolve active swimming velocities.”
More information: Eleanor K. R. Mackay et al, The Countoscope: Measuring Self and Collective Dynamics without Trajectories, Physical Review X (2024). DOI: 10.1103/PhysRevX.14.041016
Journal information: Physical Review X