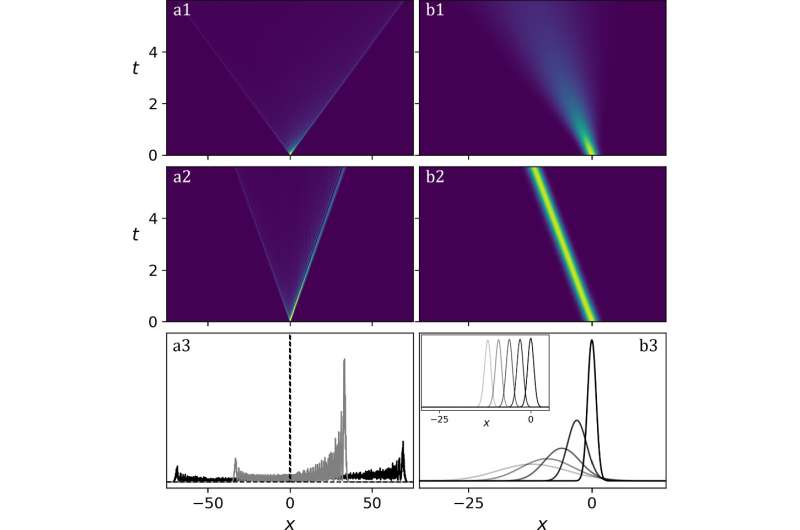
Quantum walks have been widely studied for their ability to simulate real physical phenomena. Physicists have previously studied two distinct types of quantum walk, but so far, they haven’t widely considered how their mathematical descriptions could be linked.
Through new research published in The European Physical Journal D, a pair of physicists in France— Nicolas Jolly at ENS de Lyon, and Giuseppe Di Molfetta at Aix-Marseille University—show how “discrete-time” and “continuous-time” quantum walks can be described using more general mathematical language. Their results could allow researchers to simulate an even broader range of phenomena using quantum walks.
In a classical walk, a particle moves by taking steps in different random directions—each of which has a certain probability attached to it. In contrast, a particle on a quantum walk can choose to travel in multiple directions simultaneously, according to the principles of quantum superposition.
In the past, physicists exclusively studied two different types of quantum walker. In a discrete-time walk, a system evolves in discrete steps, in which the particle performs an operation that updates its state. In contrast, the state of a continuous-time quantum walker is constantly evolving. So far, both types of quantum walker have mostly been studied through separate lines of research. Recently, however, researchers showed how both types of walker can be described using the same mathematical language. These calculations led them to a new family named “plastic” quantum walkers, which allow for both discrete-time and continuous-time behaviors.
In their latest study, Jolly and Di Molfetta introduce a more general family named “twisted” quantum walkers, named for the alteration in the choices available to them, which assume the form of plastic quantum walkers under the right conditions. In their paper, the researchers describe several important consequences for their updated theory. They ultimately hope that it could further expand the range of phenomena that can be simulated by quantum phenomena to areas including the behaviors of graphene electrons in electromagnetic fields.
More information: Nicolas Jolly et al, Twisted quantum walks, generalised Dirac equation and Fermion doubling, The European Physical Journal D (2023). DOI: 10.1140/epjd/s10053-023-00659-9
Journal information: European Physical Journal D
Provided by Springer