by Tejasri Gururaj , Phys.org
A new study published in Nature Physics introduces a theory of electron-phonon coupling that is affected by the quantum geometry of the electronic wavefunctions.
The movement of electrons in a lattice and their interactions with the lattice vibrations (or phonons) play a pivotal role in phenomena like superconductivity (resistance-free conductivity).
Electron-phonon coupling (EPC) is the interaction between free electrons and phonons, which are quasiparticles representing the vibrations of a crystal lattice. EPC leads to the formation of Cooper pairs (pairs of electrons), responsible for superconductivity in certain materials.
The new study explores the realm of quantum geometry in materials and how these can contribute to the strength of EPC.
Phys.org spoke to the first author of the study, Dr. Jiabin Yu, Moore Postdoctoral Fellow at Princeton University.
Speaking of the motivation behind the study, Dr. Yu said, “My motivation is to go beyond the common wisdom and find out how the geometric and topological properties of wavefunctions affect interactions in quantum materials. In this work, we focus on EPC, one of the most important interactions in quantum materials.”
Electronic wavefunctions and EPC
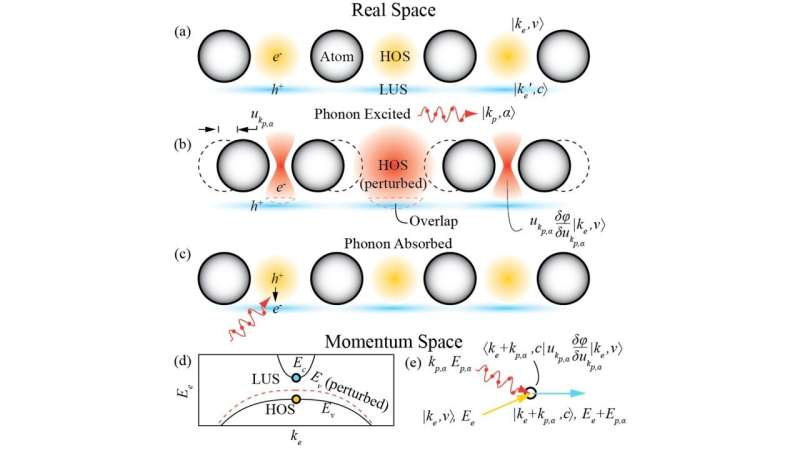
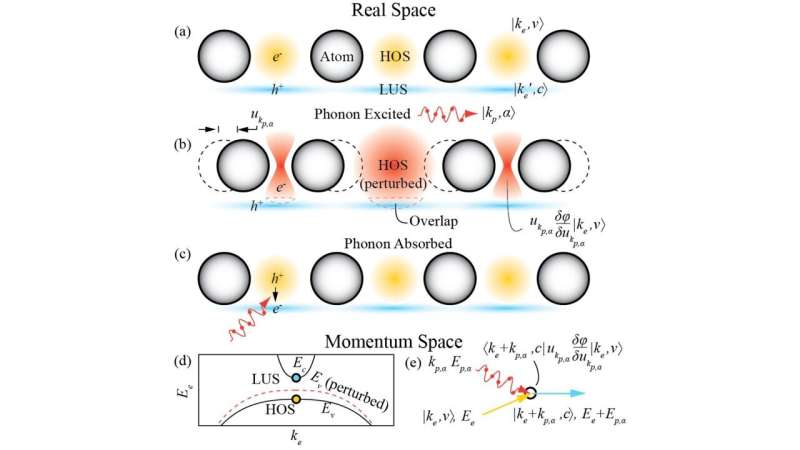
A quantum state is described by a wavefunction, a mathematical equation holding all the information about the state. An electronic wavefunction is basically a way to measure the probability of where the electron is located in the lattice (arrangement of atoms in a material).
“In condensed matter physics, people have long used energies to study the behavior of materials. In the last several decades, a paradigm shift led us to understand that the geometric and topological properties of wavefunctions are crucial in understanding and classifying realistic quantum materials,” explained Dr. Yu.
In the context of EPC, the interaction between the two depends on the location of the electron within the crystal lattice. This means that the electronic wavefunction, to some extent, governs which electrons can couple with phonons and impact the conductivity properties of that material.
The researchers in this study wanted to explore the effect of quantum geometry on the EPC in materials.
Quantum geometry
A wavefunction, as mentioned before, describes the state of a quantum particle or system.
These wavefunctions are not always static, and their shape, structure, and distribution can evolve over space and time, just like how a wave in the ocean changes. But unlike waves in the ocean, quantum mechanical wavefunctions follow the laws of quantum mechanics.
Quantum geometry explores this variation of spatial and temporal characteristics of wavefunctions.
“The geometric properties of single-particle wavefunctions are called band geometry or quantum geometry,” explained Dr. Yu.
In condensed matter physics, the band structure of materials describes the energy levels available to electrons in a crystal lattice. Think of them as steps of a ladder, with the energy increasing the higher you go.
Quantum geometry influences the band structure by affecting the spatial extent and shape of electron wavefunctions within the lattice. In simple terms, the distribution of electrons affects the energy structure or layout for electrons in a crystal lattice.
The energy levels in a lattice are crucial as they determine important properties like conductivity. Additionally, the band structure will vary from material to material.
Gaussian approximation and hopping
The researchers built their model by using Gaussian approximation. This method simplifies complex interactions (such as those between electrons and phonons) by approximating the distribution of variables like energies as Gaussian (or normal) distributions.
This makes it easier to handle mathematically and draw conclusions about the influence of quantum geometry on EPC.
“The Gaussian approximation is essentially a way to relate the real-space electron hopping to the momentum-space quantum geometry,” said Dr. Yu.
Electron hopping is a phenomenon in crystal lattices where electrons move from one site to another. For hopping to occur effectively, the wavefunctions of electrons at neighboring sites must overlap, allowing electrons to tunnel through the potential barriers between sites.
The researchers found that the overlapping was affected by the quantum geometry of the electronic wavefunction, thus affecting hopping.
“The EPC often comes from the change of the hopping with respect to the lattice vibrations. So naturally, the EPC should be enhanced by strong quantum geometry,” explained Dr. Yu.
They quantified this by measuring the EPC constant, which tells the strength of the coupling or interaction, using the Gaussian approximation.
To test their theory, they applied it to two materials, graphene and magnesium diboride (MgB2).
Superconductors and applications
The researchers chose to test their theory on graphene and MgB2 because both materials have superconducting properties driven by EPC.
They found that for both materials, EPC was strongly influenced by geometric contributions. Specifically, the geometric contributions were measured to be 50% and 90% for graphene and MgB2, respectively.
They also found the existence of a lower bound or limit for the contributions due to quantum geometry. In simple words, there is a minimum contribution towards the EPC constant due to quantum geometry, and the rest of the contribution is from the energy of the electrons.
Their work suggests that increasing superconducting critical temperature, which is the temperature below which superconductivity is observed, can be done by enhancing EPC.
Certain superconductors like MgB2 are phonon-mediated, meaning that EPC directly affects their superconducting properties. According to the research, strong quantum geometry implies strong EPC, opening a new route to search for relatively high-temperature superconductors.
“Even if EPC cannot mediate superconductivity alone, it can help cancel part of the repulsive interaction and help generate superconductivity,” added Dr. Yu.
Future work
The theory developed by the researchers has only been tested for certain materials, which means it is not universal. Dr. Yu believes that the next step is to generalize this theory to make it applicable to all materials.
This is especially important for developing and understanding different quantum materials (like topological insulators) that could be affected by quantum geometry.
“Quantum geometry is ubiquitous in quantum materials. Researchers know it should affect many quantum phenomena, but often lack theories that clearly capture this effect. Our work is one step towards such a general theory, but we are still far away from fully understanding it,” concluded Dr. Yu.
More information: Jiabin Yu et al, Non-trivial quantum geometry and the strength of electron–phonon coupling, Nature Physics (2024). DOI: 10.1038/s41567-024-02486-0.
Journal information: Nature Physics