Quantum walks are a powerful theoretical model using quantum effects such as superposition, interference and entanglement to achieve computing power beyond classical methods.
A research team at the National Innovation Institute of Defense Technology from the Academy of Military Sciences (China) recently published a review article that thoroughly summarizes the theories and characteristics, physical implementations, applications and challenges of quantum walks and quantum walk computing. The review was published Nov. 13 in Intelligent Computing in an article titled “Quantum Walk Computing: Theory, Implementation, and Application.”
As quantum mechanical equivalents of classical random walks, quantum walks use quantum phenomena to design advanced algorithms for applications such as database search, network analysis and navigation, and quantum simulations. Different types of quantum walks include discrete-time quantum walks, continuous-time quantum walks, discontinuous quantum walks, and nonunitary quantum walks. Each model presents unique features and computational advantages.
Discrete-time quantum walks involve step-by-step transitions without a time factor, using coin-based models like Hadamard and Grover walks or coinless models such as Szegedy and staggered quantum walks for graph-based movement. In contrast, continuous-time quantum walks operate on graphs using time-independent Hamiltonians, making them particularly useful for spatial searches and traversal problems.
Discontinuous quantum walks combine the properties of both discrete-time and continuous-time models, enabling universal computation through perfect state transfers. Meanwhile, nonunitary quantum walks, including stochastic quantum walks and open quantum walks, act as open quantum systems and find applications in simulating photosynthesis and quantum Markov processes.
The two original branches, discrete-time and continuous-time quantum walks, achieve faster diffusion than classical random walk models and exhibit similar probability distributions. To some extent, discrete-time and continuous-time models are interchangeable. In addition, various discrete models can be interchanged based on the graph structure, highlighting the versatility of quantum walk models.
According to the authors, quantum walks not only have evolutionary merits, but also improve sampling efficiency, solving problems previously considered computationally difficult for classical systems.
The wide variety of physical quantum systems used to implement quantum walks demonstrates the utility of discrete-time and continuous-time quantum walk models and quantum-walk-based algorithms. There are two different approaches to physically implementing quantum walks:
- Analog physical simulation primarily uses solid-state, optical and photonic systems to directly implement specific Hamiltonians without translation into quantum logic. This approach enables scalability by increasing particle numbers and dimensions but lacks error correction and fault tolerance. It faces challenges in efficiently simulating large graphs.
- Digital physical simulation constructs quantum circuits to simulate quantum walks, offering error correction and fault tolerance. Designing efficient circuits remains difficult, but digital implementations can achieve quantum speedup and simulate a variety of graphs.
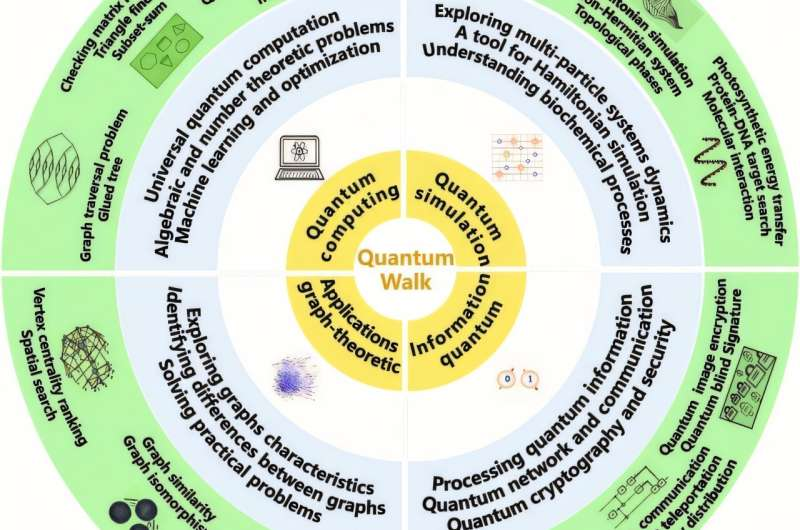
Quantum walk applications are categorized into four main categories: quantum computing, quantum simulation, quantum information processing and graph-theoretic applications.
- Quantum Computing: Quantum walks enable universal quantum computation and accelerate computations in algebraic and number-theoretic problems. They are also being explored for applications in machine learning and optimization.
- Quantum Simulation: Quantum walks are an important tool for simulating the behavior of uncontrollable quantum systems, providing insight into complex quantum phenomena that are difficult or impossible to analyze classically. Applications include simulating multi-particle systems, solving complex physics problems, and modeling biochemical processes.
- Quantum Information Processing: Quantum walks are used for the preparation, manipulation, characterization and transmission of quantum states, as well as in quantum cryptography and security applications.
- Graph-Theoretic Applications: Quantum walks, associated with graph structures, provide promising solutions for graph-theoretic problems and various network applications. They are used to explore graph characteristics, rank vertex centrality and identify structural differences between graphs.
Despite rapid progress, practical quantum walk computing faces challenges, including devising effective algorithms, scaling up the physical implementations and implementing quantum walks with error correction or fault tolerance. These challenges, however, provide a roadmap for future innovations and advancements in the field.
More information: Xiaogang Qiang et al, Quantum Walk Computing: Theory, Implementation, and Application, Intelligent Computing (2024). DOI: 10.34133/icomputing.0097
Provided by Intelligent Computing
