New research conducted by Princeton University physicists is delving with high resolution into the complex and fascinating world of topological quantum matter—a branch of physics that studies the inherent quantum properties of materials that can be deformed but not intrinsically changed. By repeating an experiment first conducted by researchers at Kyoto University, the Princeton team has clarified key aspects of the original experiment, and importantly, reached novel and divergent conclusions—conclusions that advance our understanding of topological matter.
As chronicled in a paper published in the journal Nature Materials, the Princeton researchers used a special type of magnetic insulator realized in ruthenium chloride (α-RuCl3) to demonstrate the first example of a magnetic insulator that exhibits the thermal Hall effect arising from quantum edge modes of bosons in the presence of a novel force field called the Berry curvature.
Background to the experiment
The experiment has its origins in the work of Princeton physicist and 1977 Nobel Prize-winner Phil Anderson, who theorized a novel state of matter called spin liquids. These are classes of magnetic materials that—even under extremely low temperatures—do not undergo what physicists call a magnetic phase transition. This describes an abrupt transition to a state in which the spin at each lattice site either aligns in a perfectly parallel pattern, called ferromagnetic order, or alternates in an orderly fashion between up and down, called antiferromagnetic order. Over ninety-nine percent of magnetic materials experience this phase transition when cooled to sufficiently low temperatures. Anderson suggested the term “geometric frustration” to describe how spin liquids are prevented from undergoing such phase transitions.
“To illustrate this concept, imagine trying to seat couples around a dinner table under the rule that every woman is to be seated between two men and vice versa,” said N. Phuan Ong, the Eugene Higgins Professor of Physics at Princeton University and the senior author of the paper. “If we have a guest who arrives alone, this arrangement is geometrically impossible.”
In 2006, Russian physicist Alexei Kitaev at the California Institute of Technology (Caltech) proposed that Anderson’s spin liquid state could be achieved without invoking Anderson’s concept of geometric frustration. He outlined this in a series of elegant equations, and importantly, predicted the existence of new particles called Majoranas and visons. The Majorana particle is an especially strange and elusive subatomic particle that was first theorized in 1937 by Italian physicist Ettore Majorana. It is a type of fermion; in fact, it is the only fermion recognized as identical to its own antiparticle.
Kitaev’s work sparked a flurry of research to find materials that could realize his model calculations in the laboratory. Two years later, two physicists, George Jackeli and Giniyat Khailyulin of the Max Planck Institute in Stuttgart, Germany, predicted ruthenium chloride (α-RuCl3) to be the closest proximate. This material, which crystallizes in a honeycomb lattice, is an excellent insulator.
Consequently, in the past decade, α-RuCl3 has become one of the most intensively investigated candidates for quantum spin liquids. The research received a considerable boost in 2018 when physicist Yuji Matsuda and his colleagues at Kyoto University reported the observation of the “half-quantized” thermal Hall effect predicted in Kitaev’s calculations.
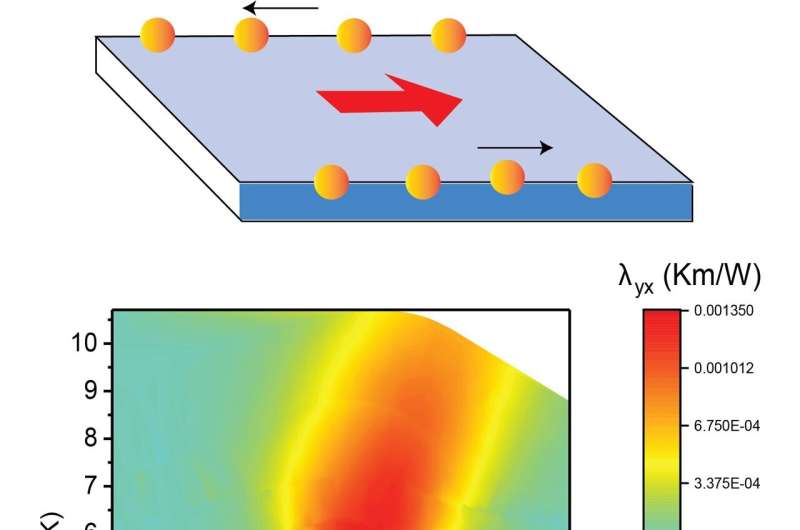
The thermal Hall effect, which is analogous to the more familiar electrical Hall effect, describes how an intense magnetic field deflects sideways an applied heat current. The sideways deflection engenders a weak temperature difference between two edges of the sample, which reverses sign if the direction of the magnetic field is reversed. While the thermal Hall effect is well established in metals such as copper and gallium, it is very rarely observed in insulators. This is because, in insulators, a heat current is conveyed by lattice vibrations called phonons that are indifferent to the magnetic field, Ong noted.
Matsuda reported that their measurements of the thermal Hall conductivity revealed that it was “half-quantized.” The magnitude depends only on the Planck constant and the Boltzmann constant, and nothing else, as predicted by Kitaev. “This experiment, implying the observation of a current of Majorana particles, attracted enormous interest in the community.”
But Ong and his research team, long familiar with thermal Hall experiments, felt that there was something amiss with Matsuda’s conclusion. “I couldn’t quite put my finger on it,” Ong said.
The experiment
Ong and his colleagues decided to repeat the experiment. But this time, they aimed to conduct the experiment at a higher resolution and over a much larger temperature interval—from one-half degrees Kelvin to ten degrees Kelvin.
The high level of resolution was critical to the success of the experiment, explained Peter Czajka, the lead author of the paper and a graduate student in physics. “Our experiment is a great example of something that is conceptually quite simple, but very difficult in practice. It’s relatively easy to measure the electrical resistance of something but measuring the thermal conductivity of a sample is much harder.”
The first part of the experiment required the researchers to select a sample of ruthenium chloride that had several specific characteristics, including a very thin crystal structure with a distinct hexagonal shape. They then attached sensitive thermometers to measure the temperature gradients.
“All we’re really doing is measuring very small temperature gradients on a crystal,” said Czajka. “But to do this we need a resolution of a thousandth to a millionth of a degree—something in between that scale.”
The researchers cooled the material down to temperatures of one Kelvin or lower, and subjected the sample to a strong magnetic field, which was applied parallel to the heat current. They then used an electrical heater to warm up one edge of the crystal and measured the temperature gradients. The experiment—measurements of temperature gradients—required, amazingly, a period of several months.
“The sample was cold for about six months,” said Czajka, “and during that time we thoroughly mapped out the temperature and field dependence. This was unprecedented because most researchers aren’t willing to put six months into a single experiment.”
The first thing the researchers noticed, in a finding parallel with Matsuda’s, was the presence of the thermal Hall effect. The researchers recognized this when the thermometers detected that the flow of the heat current was deflected to one side or the other depending on the magnetic field.
To explain this, Ong used the analogy of a raft going downstream, with the river current symbolizing the heat current and the raft symbolizing a packet of heat entropy. “Although you’re going with the flow of the river, you find that your raft is being pushed to one side of the river, say the left bank. And all the rafts following you are similarly being pushed to the left bank,” he said. This leads to a slight increase in the left bank’s temperature.
The signal is also sensitive to the direction of the magnetic field, said Ong. “If you repeat the experiment with the magnetic field reversed in direction, you will find all the rafts, which are still going downstream, accumulating on the right bank.”
In the vast majority of insulators, this effect does not occur. “The rafts will not accumulate on either the left or right side; they will just flow down the river,” said Ong.
But in these new topological materials the effect is startling. And the reason for this is because of a phenomenon known as the Berry curvature.
In principle, all crystalline materials display an internal force field called the Berry curvature, named after Michael Berry, a mathematical physicist at the University of Bristol. The Berry Curvature describes how wave functions twist and turn throughout the space spanned by momentum. In magnetic and topological materials, the Berry curvature is finite. It acts on charged particles, such as electrons, as well as neutral ones, such as phonons and spins, much like an intense magnetic field.
“The Berry curvature is a concept that was missing for the last sixty years, but has now come to the fore in the last five years or so,” said Ong. “It’s the Berry Curvature that we proved in this paper that is actually the cause of Matsuda’s experimental observation.”
Equally important, the Princeton researchers were not able to confirm the presence of the Majorana fermion, as originally predicted in Matsuda’s experiment. Rather, the researchers traced the thermal Hall effect to another kind of particle, a boson.
All particles in nature are either fermions or bosons. Electrons are fermions, while particles such as photons, phonons and gluons are bosons. Bosons originate from the wave-like collective excitations of the magnetic moments at high magnetic field. Both types of particles can give rise to the thermal Hall effect if the materials used are topological in nature.
“In our study, we demonstrate rather convincingly that the observed particles are bosons rather than fermions,” said Ong. “If the Kyoto group had been correct—if the particles were identified as fermions—the signal would be independent of temperature. But the signal is, in fact, strongly temperature dependent, and its temperature dependence very precisely corresponds to a quantitative model for topological boson excitations.”
“Our experiment is the first example of what is called a bosonic material displaying quantum edge transport,” Ong added.
Implications and future research
Ong and his team believe their research has robust implications for fundamental physics research.
“What our experiment accomplished—by clarifying the presence of bosons rather than fermions—is to open the door to using the thermal Hall effect in the same way that the quantum Hall Effect has been used to uncover many novel quantum states,” said Ong.
Ong also said that the particles discovered in experiments like this one might have practical applications for such things as topological quantum computing or quantum devices, though achieving such breakthroughs are likely twenty or more years down the road. Ong and the members of his research laboratory intend to continue their research by searching for similar bosonic Hall effects in related materials, and study the quantum possibilities of ruthenium chloride in even greater detail. The experiments were performed in collaboration with scientists at Oak Ridge National Laboratories, the University of Tennessee, Tokyo University and Purdue University.
More information: Peter Czajka et al, Planar thermal Hall effect of topological bosons in the Kitaev magnet α-RuCl3, Nature Materials (2022). DOI: 10.1038/s41563-022-01397-w
Provided by Princeton University

